网络流--Dinic算法

更新于: | 阅读次数: | 评论数:
字数统计: 2k | 阅读时长 ≈ 9

Dinic算法

例题:CodeVS 1993 草地排水

题目描述 Description
在农夫约翰的农场上，每逢下雨，Bessie最喜欢的三叶草地就积聚了一潭水。这意味着草地被水淹没了，并且小草要继续生长还要花相当长一段时间。因此，农夫约翰修建了一套排水系统来使贝茜的草地免除被大水淹没的烦恼（不用担心，雨水会流向附近的一条小溪）。作为一名一流的技师，农夫约翰已经在每条排水沟的一端安上了控制器，这样他可以控制流入排水沟的水流量。

农夫约翰知道每一条排水沟每分钟可以流过的水量，和排水系统的准确布局（起点为水潭而终点为小溪的一张网）。需要注意的是，有些时候从一处到另一处不只有一条排水沟。

根据这些信息，计算从水潭排水到小溪的最大流量。对于给出的每条排水沟，雨水只能沿着一个方向流动，注意可能会出现雨水环形流动的情形。

输入描述 Input Description
第1行: 两个用空格分开的整数N (0 <= N <= 200) 和 M (2 <= M <= 200)。N是农夫John已经挖好的排水沟的数量，M是排水沟交叉点的数量。交点1是水潭，交点M是小溪。

第二行到第N+1行: 每行有三个整数，Si, Ei, 和 Ci。Si 和 Ei (1 <= Si, Ei <= M) 指明排水沟两端的交点，雨水从Si 流向Ei。Ci (0 <= Ci <= 10,000,000)是这条排水沟的最大容量。

输出描述 Output Description
输出一个整数，即排水的最大流量。

样例输入 Sample Input
5 4
1 2 40
1 4 20
2 4 20
2 3 30
3 4 10

样例输出 Sample Output
50

问题分析

很显然，这是一道网络流问题，源点为1号节点，汇点为第n号节点，中间的点之间由有向边连接，边权即为流量wi，这样就简单构造了一个网络流的问题，由于题目要求排水的最大流量，也就是求出此网络中的最大流。

对于求最大流的问题，大家入门时一定接触的是EK算法，但是EK算法的效率实在感人，难以满足竞赛中的需要，而Dinic算法通过对EK算法简单的优化使其效率有了明显的提升，基本能够满足竞赛对求最大流的效率的要求。那么Dinic是怎样优化的呢？

Dinic算法有三个关键词：增广路，残量网络，层次。

首先，增广路就是每次从源点扩展一条可以到汇点的路径，然后更新一遍残留网络后继续寻找一条这样的路径的过程直至从源点到汇点没有一条路径可达时停止，这个过程就是求增广路的过程。（附上一组求增广路的流程图）

增广路

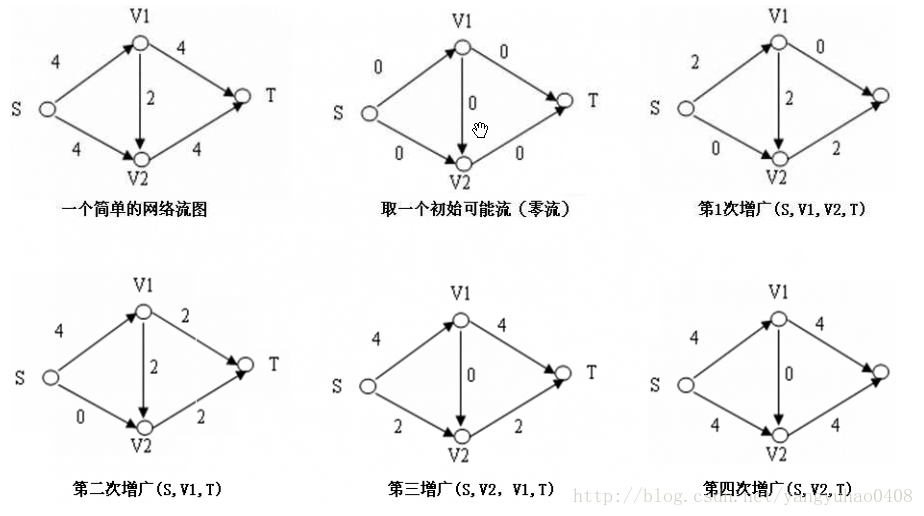
残量网络是Dinic算法（也是EK算法）的关键，残量网络实际上就是流网络上一条边在当前流量的基础上可以允许的额外流量，即 $C_f(u,v)=c(u,v) -f(u,v)$ 但需要特别注意的是，当 $C_f(u,v)$ 为0时该条边将不属于图 $ G_f $。残量网络的构建相当于给了你一个后悔的机会，将原来已经删去的路在可以得到更优解时换回来，即将反向弧再次反向，又回到原来的状态。

之前两点并不是Dinic算法独有的，EK算法同样需要，然而Dinic更优秀的地方就在于第三点，它求增广路前先将图进行分层，逐层递进寻找增广路，这样每条路都是s-t最短路，根据最短增广路算法中的证明（不必深究），可以确定这样找增广路的效率得到大幅提高！

代码

了解了算法的关键，码出来也不会有太大障碍，每次增光前bfs分一次层即可，下面附上代码(邻接矩阵存储)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define maxn 255
using namespace std;
const int INF=0x3f3f3f3f;
int n,m;
int edge[maxn][maxn];
int now[maxn],dis[maxn];

int bfs()										//分层
{
	memset(dis,-1,sizeof(dis));
	queue<int > q;
	q.push(1);
	dis[1]=0;
	while(!q.empty())
	{
		int u=q.front() ;
		q.pop();
		for(int i=1;i<=n;++i)
		{
			if(dis[i]==-1 && edge[u][i]>0)
			{
				dis[i]=dis[u]+1;
				q.push(i);
			}
		}
	} 
	return dis[n]==-1?0:dis[n];
}

int MaxFlow(int u,int flow)
{
	if(u==n) return flow;
	int post_maxflow;
	for(int i=now[u];i<n;++i)                    //当前弧优化
	{
		now[u]=1;
		if(dis[i+1]==dis[u]+1 && edge[u][i+1]>0 && (post_maxflow=MaxFlow(i+1,min(flow,edge[u][i+1]))))
		{
			edge[u][i+1]-=post_maxflow; 
			edge[i+1][u]+=post_maxflow;
			return post_maxflow;
		}
	}
	return 0;
}

int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	int sumflow=0;
	memset(edge,0,sizeof(edge));
	scanf("%d%d",&m,&n);
	for(int i=1;i<=m;++i)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		edge[u][v]+=w;
	}
	while(bfs())
	{
		int flow;
		memset(now,0,sizeof(now));
		while(flow=MaxFlow(1,INF)) sumflow+=flow;
	}
	printf("%d",sumflow);
	return 0;
}

但是当图很大时，邻接矩阵显然无法满足我们的需求，如POJ3469 Dual Core CPU 中 n<=20000,这时再用邻接矩阵会ML，只要将图该用邻接表存储即可，附上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>

#define Repeat(s,t) for(int i=(s);i<(t);++i)
#define INF 0x3f3f3f3f
#define maxn 20000+50

#define DEBUG
using namespace std;

struct edge
{
	int from,to,cap,flow;
	edge(int from,int to,int cap,int flow):from(from),to(to),cap(cap),flow(flow) {}
};

struct dinic
{
	int n,m,s,t;
	vector<edge> edges;
	vector<int> G[maxn];
	int d[maxn];
	int cur[maxn];
	dinic() {}
	
	void init()
	{
		memset(d,-1,sizeof(d));
		memset(cur,0,sizeof(0));
	}
	
	void add_edge(int from,int to,int cap,int flag)
	{
		if(!flag)
		{
		edges.push_back(edge(from,to,cap,0));
		edges.push_back(edge(to,from,0,0));
		}
		else
		{
		edges.push_back(edge(from,to,cap,0));
		edges.push_back(edge(to,from,cap,0));  
		}
		m=edges.size();
		G[from].push_back(m-2);
		G[to].push_back(m-1);    
	}
	
	bool bfs()
	{
		memset(d,-1,sizeof(d));
		queue<int> q;
		q.push(s);
		d[s]=0;
		while(!q.empty())
		{
			int u=q.front() ;
			q.pop();
			for(unsigned int i=0;i<G[u].size();++i)
			{
				edge& e=edges[G[u][i]];
				if(d[e.to]==-1 && e.cap>e.flow)
				{
					d[e.to]=d[u]+1;
					q.push(e.to);
				}
			}
		} 
		return d[t]==-1?0:1;
	}
	
	int dfs(int x,int a)
	{	
		if(x==t || a==0) return a;
		int flow=0,f;
		for(unsigned int i=cur[x];i<G[x].size();++i)
		{
			cur[x]=i;
			edge& e=edges[G[x][i]];
			if(d[x]+1==d[e.to] && (f=dfs(e.to,min(a,e.cap-e.flow)))>0)
			{
				e.flow+=f;
				edges[G[x][i]^1].flow-=f;
				flow+=f;
				a-=f;
				if(a==0) break;
			}
		}
		return flow;
	}
	
	int MaxFlow(int n,int s,int t)
	{
		this->n=n;
		this->s=s;
		this->t=t;
		int flow=0;
		while(bfs())
		{
			memset(cur,0,sizeof(cur));
			flow+=dfs(s,INF);
		}
		return flow;
	}
};

inline int read()
{
	/*神tm一定要注意过滤掉数据前面的多余空格或者换行符!否则会导致不可名状的错误!po主付出过惨痛代价QAQ*/
	char ch;
	do
		ch=getchar();
	while((ch < '0' || ch > '9') && ch !='-');
	int read=0;
	bool sign=0;
	if(ch=='-')
	{
		sign=1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9')
	{
		read=read*10+ch-'0';
		ch=getchar();
	}
	return sign==0?read:-read;
}

inline void write(int out)
{
	if(out<0)
	{
		putchar('-');
		out=-out;
	}
	if(out>9) write(out/10);
	putchar(out%10+'0');
}

int main()
{
	int n,m;
	n=read();
	m=read();
	int s=0,t=n+1;
	dinic D;
	Repeat(1,n+1)
	{
		int a=read(),b=read();
		D.add_edge(s,i,a,0);
		D.add_edge(i,t,b,0); 
	}
	Repeat(1,m+1)
	{
		int a=read(),b=read(),w=read();
		D.add_edge(a,b,w,1); 
	}
	write(D.MaxFlow(n,s,t));
	return 0;
}
-------------本文结束感谢您的阅读-------------